Detaljerad analys av RC -seriekretsen
2024-05-08
20588
RC -seriekretsen, bestående av ett motstånd och en kondensator, fungerar som en grundläggande komponent i både grundläggande och avancerade elektroniska systemkonstruktioner.Det hjälper till att förstå viktiga principer som frekvensrespons, fasskift och signalfiltrering, som spelar en viktig roll i kretsdesign och signalbehandling.Denna utforskning täcker teoretiska grunder och sträcker sig till praktiska tillämpningar genom experiment och simuleringar.Genom att fysiskt montera kretsen eller modellera den digitalt kan eleverna visuellt förstå laddningsprocessen och effekterna av komponent V ariat -joner, vilket gör komplexa koncept mer tillgängliga och minnesvärda.
Katalog

Bild 1: Olika utgångsspänningar för RC -kretsar
Introduktion till RC -krets
En RC-krets, kort för motståndskapacitanskrets, är grundläggande i elektronik för att manipulera signaler genom motstånd och kondensatorer.Dessa kretsar är särskilt kända för sin förmåga att skifta faser och filtersignaler med enkla arrangemang av dessa komponenter.En grundläggande RC-krets, ofta kallad en första ordning RC-krets, innehåller vanligtvis bara ett motstånd och en kondensator.
I en typisk installation appliceras ingångsspänningen på serieforrettet av ett motstånd och en kondensator.Utgången kan dras antingen över motståndet eller kondensatorn, var och en ger olika svar på signalfrekvenser på grund av kondensatorns unika egenskaper.Denna mångsidighet gör det möjligt för RC -kretsar att utföra en mängd olika roller i elektroniska enheter, såsom kopplings- och filtreringssignaler eller till och med konvertera vågformer när de utsätts för en stegspänning.
RC-kretsen kan konfigureras på flera sätt-serier, parallella eller en kombination av båda, känd som serie-parallell.Varje konfiguration påverkar signalfrekvenser på olika sätt: Seriesanslutningar tenderar att dämpa låga frekvenser, medan parallella anslutningar används för att dämpa högre frekvenser.Denna skillnad beror främst på hur motstånd och kondensatorer interagerar med kretsen;Motstånd motsätter sig direkt ström medan kondensatorer lagrar och släpper det, vilket påverkar hur kretsen svarar på olika frekvenser.
Till skillnad från kretsar som inkluderar induktorer, som LC -kretsar, kan enkla RC -kretsar inte resonera eftersom motstånd inte lagrar energi.Detta attribut påverkar tydligt hur RC -kretsar används, med fokus på deras kapacitet för filtrering snarare än energilagring eller resonans.Varje konfiguration tjänar ett specifikt syfte, vilket gör RC -kretsar mångsidiga verktyg i både teoretisk studie och praktisk tillämpning i elektronisk design.
RC Series Circuit
En RC -seriekrets, i huvudsak sammansatt av ett motstånd (R) och en kondensator (C) I serie fungerar på en enkel princip.När kretsens omkopplare är stängd börjar kondensatorn ladda från den applicerade spänningen (V), initiera ett strömflöde genom kretsen.När kondensatorn laddas ökar strömmen gradvis tills kondensatorn når sin kapacitet, vid vilken tidpunkt den slutar acceptera laddningen, och den nuvarande stabiliseras till dess maximala värde, beräknat som  .
.
 .
.Laddningsprocessen för kondensatorn kan matematiskt beskrivas av ekvationen 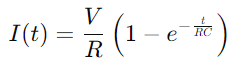 , där jag är den nuvarande, V är spänningen, R är motståndet, C är kapacitansen, t är tid och e är basen för den naturliga logaritmen.Denna formel återspeglar hur strömmen förändras över tid när kondensatorn laddas, med produkten av motstånds- och kapacitansvärden (RC) som definierar kretsens tidskonstant, vilket indikerar hastigheten med vilken kondensatorn laddas.
, där jag är den nuvarande, V är spänningen, R är motståndet, C är kapacitansen, t är tid och e är basen för den naturliga logaritmen.Denna formel återspeglar hur strömmen förändras över tid när kondensatorn laddas, med produkten av motstånds- och kapacitansvärden (RC) som definierar kretsens tidskonstant, vilket indikerar hastigheten med vilken kondensatorn laddas.
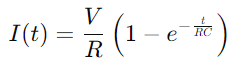 , där jag är den nuvarande, V är spänningen, R är motståndet, C är kapacitansen, t är tid och e är basen för den naturliga logaritmen.Denna formel återspeglar hur strömmen förändras över tid när kondensatorn laddas, med produkten av motstånds- och kapacitansvärden (RC) som definierar kretsens tidskonstant, vilket indikerar hastigheten med vilken kondensatorn laddas.
, där jag är den nuvarande, V är spänningen, R är motståndet, C är kapacitansen, t är tid och e är basen för den naturliga logaritmen.Denna formel återspeglar hur strömmen förändras över tid när kondensatorn laddas, med produkten av motstånds- och kapacitansvärden (RC) som definierar kretsens tidskonstant, vilket indikerar hastigheten med vilken kondensatorn laddas.
Bild 2: RC -seriekrets
Utsläpp inträffar när omkopplaren öppnas och vänder processen: den lagrade energin i kondensatorn frigörs, vilket får strömmen att flyta i motsatt riktning tills kondensatorn är tömd.Denna laddnings- och urladdningscykel är avgörande i applikationer som signalomvandling, filtrering och tidskretsar på grund av det förutsägbara sättet på vilket ström- och spänningsändringen.

Bild 3: RC -serie kortslutning
Beteendet hos RC -seriekretsen varierar också med frekvens.Vid låga frekvenser fungerar kondensatorn mer som en öppen krets, vilket i hög grad hindrar strömflödet.När frekvensen ökar minskar den kapacitiva reaktansen, vilket gör det lättare för strömmen att passera igenom.Denna förändring i impedans med frekvens gör det möjligt för RC -seriekretsen att fungera som ett filter, selektivt dämpande frekvenser under en viss tröskel (svängfrekvens  ).
).
 ).
).
Bild 4: Laddning och urladdning av RC -seriekretsar
Förutom stabila operationer studeras också RC-kretsar för sina övergående svar när de utsätts för plötsliga spänningsförändringar, till exempel när en likströmsförsörjning är på eller av.Detta scenario benämns en övergående process, där kretsen övergår från ett stabilt tillstånd till ett annat.Dynamiken i denna process beror avsevärt på RC -tidskonstanten, vilket styr hur snabbt kretsen reagerar på förändringar.
I slutändan tjänar RC -seriekretsar flera funktioner i både DC- och AC -applikationer, och hanterar uppgifter som sträcker sig från att försena signaler till integrering eller koppling av olika kretselement.Denna mångsidighet härrör från de unika interaktionerna mellan motståndet och kondensatorn, som tillsammans bestämmer kretsens övergripande svar på förändringar i spänning och frekvens.

Bild 5: RC -seriekretsdiagram och frekvensformel
I en RC -seriekrets, samspelet mellan motståndet (R) och kondensatorn (C) påverkar både strömflödet och spänningsfördelningen.Motståndets primära roll är att reglera det nuvarande flödet.Detta förhållande kvantifieras av Ohms lag, som säger 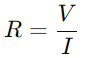 , var V är spänning och Jag är aktuell.I huvudsak fungerar motståndet som en flaskhals och kontrollerar hur mycket el som kan gå igenom vid varje given tidpunkt.
, var V är spänning och Jag är aktuell.I huvudsak fungerar motståndet som en flaskhals och kontrollerar hur mycket el som kan gå igenom vid varje given tidpunkt.
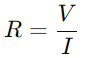 , var V är spänning och Jag är aktuell.I huvudsak fungerar motståndet som en flaskhals och kontrollerar hur mycket el som kan gå igenom vid varje given tidpunkt.
, var V är spänning och Jag är aktuell.I huvudsak fungerar motståndet som en flaskhals och kontrollerar hur mycket el som kan gå igenom vid varje given tidpunkt.Kondensatorns funktion är något mer komplicerad eftersom den tillfälligt lagrar elektrisk energi och sedan släpper tillbaka den in i kretsen.Spänningen över kondensatorn (Vc) korrelerar med sin lagrade laddning (Q) och beräknas med formeln 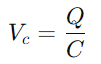 .Detta förhållande belyser kondensatorns förmåga att hålla laddningen och påverkar direkt den spänning den visar.Under drift är dynamiken i laddning och urladdning av kondensatorn avgörande för att förstå RC -kretsar.Tidskonstanten (τ), definierad som
.Detta förhållande belyser kondensatorns förmåga att hålla laddningen och påverkar direkt den spänning den visar.Under drift är dynamiken i laddning och urladdning av kondensatorn avgörande för att förstå RC -kretsar.Tidskonstanten (τ), definierad som 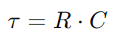 , mäter hur snabbt kondensatorn når cirka 63,2% av den fulla spänningen som tillhandahålls av källan (V0).Denna tid är konstant indikativ på hur kretsen anpassar sig till inmatningsändringar, med motståndet och kondensatoregenskaperna som dikterar takten i dessa justeringar.
, mäter hur snabbt kondensatorn når cirka 63,2% av den fulla spänningen som tillhandahålls av källan (V0).Denna tid är konstant indikativ på hur kretsen anpassar sig till inmatningsändringar, med motståndet och kondensatoregenskaperna som dikterar takten i dessa justeringar.
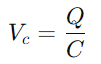 .Detta förhållande belyser kondensatorns förmåga att hålla laddningen och påverkar direkt den spänning den visar.Under drift är dynamiken i laddning och urladdning av kondensatorn avgörande för att förstå RC -kretsar.Tidskonstanten (τ), definierad som
.Detta förhållande belyser kondensatorns förmåga att hålla laddningen och påverkar direkt den spänning den visar.Under drift är dynamiken i laddning och urladdning av kondensatorn avgörande för att förstå RC -kretsar.Tidskonstanten (τ), definierad som 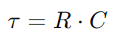 , mäter hur snabbt kondensatorn når cirka 63,2% av den fulla spänningen som tillhandahålls av källan (V0).Denna tid är konstant indikativ på hur kretsen anpassar sig till inmatningsändringar, med motståndet och kondensatoregenskaperna som dikterar takten i dessa justeringar.
, mäter hur snabbt kondensatorn når cirka 63,2% av den fulla spänningen som tillhandahålls av källan (V0).Denna tid är konstant indikativ på hur kretsen anpassar sig till inmatningsändringar, med motståndet och kondensatoregenskaperna som dikterar takten i dessa justeringar.Spänningen över kondensatorn vid varje givet ögonblick under laddningen ges av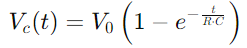 , illustrerar en icke-linjär ökning när kondensatorn fylls.Denna ekvation beskriver hur laddningshastigheten bromsar när kondensatorn närmar sig full kapacitet.
, illustrerar en icke-linjär ökning när kondensatorn fylls.Denna ekvation beskriver hur laddningshastigheten bromsar när kondensatorn närmar sig full kapacitet.
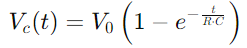 , illustrerar en icke-linjär ökning när kondensatorn fylls.Denna ekvation beskriver hur laddningshastigheten bromsar när kondensatorn närmar sig full kapacitet.
, illustrerar en icke-linjär ökning när kondensatorn fylls.Denna ekvation beskriver hur laddningshastigheten bromsar när kondensatorn närmar sig full kapacitet.Omvänt, under urladdning, minskar kondensatorns spänning enligt  , framställer en linjär minskning av lagrad energi över tid.Denna process ger en tydlig bild av hur energi frigörs från kondensatorn tillbaka till kretsen.I växelströmsapplikationer, fasskillnaden mellan spänningen och strömmen, φ, blir kritisk.Denna skillnad, beräknad som
, framställer en linjär minskning av lagrad energi över tid.Denna process ger en tydlig bild av hur energi frigörs från kondensatorn tillbaka till kretsen.I växelströmsapplikationer, fasskillnaden mellan spänningen och strömmen, φ, blir kritisk.Denna skillnad, beräknad som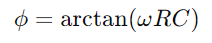 där Ω Representerar vinkelfrekvensen, visar förseningen som orsakas av kondensatorn, vilket påverkar tidpunkten mellan strömflöden och spänningsändringar över komponenterna.
där Ω Representerar vinkelfrekvensen, visar förseningen som orsakas av kondensatorn, vilket påverkar tidpunkten mellan strömflöden och spänningsändringar över komponenterna.
 , framställer en linjär minskning av lagrad energi över tid.Denna process ger en tydlig bild av hur energi frigörs från kondensatorn tillbaka till kretsen.I växelströmsapplikationer, fasskillnaden mellan spänningen och strömmen, φ, blir kritisk.Denna skillnad, beräknad som
, framställer en linjär minskning av lagrad energi över tid.Denna process ger en tydlig bild av hur energi frigörs från kondensatorn tillbaka till kretsen.I växelströmsapplikationer, fasskillnaden mellan spänningen och strömmen, φ, blir kritisk.Denna skillnad, beräknad som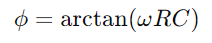 där Ω Representerar vinkelfrekvensen, visar förseningen som orsakas av kondensatorn, vilket påverkar tidpunkten mellan strömflöden och spänningsändringar över komponenterna.
där Ω Representerar vinkelfrekvensen, visar förseningen som orsakas av kondensatorn, vilket påverkar tidpunkten mellan strömflöden och spänningsändringar över komponenterna.Sammantaget begränsar motståndet och riktar strömflödet medan kondensatorn lagrar och modulerar spänningen.Tillsammans bestämmer de kretsens svaregenskaper, till exempel hur snabbt den kan ladda och urladdning och fasförändringarna som inträffar i växlande nuvarande scenarier.Detta kombinerade beteende understödjer de grundläggande operationerna i RC -serien kretsar, vilket gör dem integrerade i olika elektroniska applikationer.
Grundläggande ekvationer av RC -serien kretsar
För att förstå beteendet hos en RC -seriekrets är det avgörande att börja med de grundläggande ekvationerna som beskriver dess svar på förändringar i ingångsspänningen.Antag att vi har en byte av ingångsspänning representerad som Vin (t)med spänningen över motståndet märkt som VR (t) och över kondensatorn som Vc (t).I en seriekrets, samma ström, Det) flyter genom både motståndet och kondensatorn.
Tillämpning av Kirchhoffs spänningslag (KVL), som säger att den totala spänningen runt alla stängda slinga i en krets måste vara lika med noll, finner vi att ingångsspänningen är lika med summan av spänningarna över motståndet och kondensatorn:

Spänningen över motståndet kan beräknas med Ohms lag:
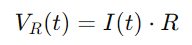
För kondensatorn är spännings VC (t) relaterad till laddningen q (t) den har, ges av:
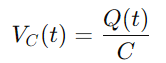
Eftersom strömmen definieras som laddningsfrekvensen har vi:
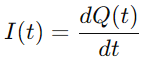
Genom att ersätta Q (t) i ekvationen för Vc (t)och använder derivatet av laddning Det), Vi härleder kärndifferentialekvationen för RC -seriens krets:

Ytterligare ersättning Q (t) med integrationen av Det), vi får:
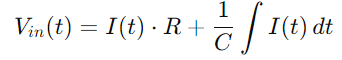
För strömmen i (t), med tanke på spänningshastigheten över kondensatorn, använder vi:
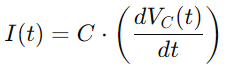
Integrering av alla dessa förhållanden ger oss den differentiella ekvationen som beskriver spänningen över kondensatorn:

Detta är en första ordning linjär differentiell ekvation som fångar den tidsberoende spänningsförändringen över kondensatorn.Att lösa denna ekvation gör att vi exakt kan beskriva hur kondensatorspänningen utvecklas.Denna förståelse är grundläggande för att analysera både laddnings- och urladdningscyklerna för kondensatorn, liksom kretsens svar på olika frekvenser.Denna omfattande strategi ger en djup inblick i de dynamiska egenskaperna hos RC -serien.

Bild 6: Spänningsdifferentialekvation
Impedans av RC -serie krets
För att skriva om beskrivningen av en RC-seriekrets, med fokus på mänsklig interaktion och en direkt, förenklad förklaring, låt oss förbättra de konkreta upplevelserna och steg-för-steg-operationerna samtidigt som vi upprätthåller kärnmeddelandet och sammanhållningen:
I en RC -seriekrets arbetar motståndet och kondensatorn i tandem för att kontrollera flödet av el, avgörande när man hanterar växlande strömmar.Kretsens totala impedans, representerad som  , kombinerar motståndet R och den kapacitiva reaktansen XC.Den viktigaste funktionen med denna installation är att impedansvärdena för båda komponenterna varierar med frekvensförändringar.När frekvensen ökar minskar kondensatorns impedans, vilket gör att mer ström kan passera, medan motståndet i huvudsak förblir konstant.
, kombinerar motståndet R och den kapacitiva reaktansen XC.Den viktigaste funktionen med denna installation är att impedansvärdena för båda komponenterna varierar med frekvensförändringar.När frekvensen ökar minskar kondensatorns impedans, vilket gör att mer ström kan passera, medan motståndet i huvudsak förblir konstant.
 , kombinerar motståndet R och den kapacitiva reaktansen XC.Den viktigaste funktionen med denna installation är att impedansvärdena för båda komponenterna varierar med frekvensförändringar.När frekvensen ökar minskar kondensatorns impedans, vilket gör att mer ström kan passera, medan motståndet i huvudsak förblir konstant.
, kombinerar motståndet R och den kapacitiva reaktansen XC.Den viktigaste funktionen med denna installation är att impedansvärdena för båda komponenterna varierar med frekvensförändringar.När frekvensen ökar minskar kondensatorns impedans, vilket gör att mer ström kan passera, medan motståndet i huvudsak förblir konstant.Impedansen, betecknad som Z och mätt i ohm (ω), spelar en kritisk roll för att bestämma hur kretsen reagerar på växelström.Som i RL -seriekretsar, motståndet R och kapacitiv reaktans xC av en RC -krets bildar en triangel känd som impedansstriangeln.Denna triangel hänför sig nära spännings triangeln, och genom att tillämpa Pythagorean -teoremet kan du beräkna kretsens totala impedans.

Bild 7: RC -seriekretsberäkningsformel
När det gäller praktiska tillämpningar kan du överväga hörlurar som använder dessa principer.Högimpedans hörlurar, som ofta överstiger 200 ohm, används vanligtvis med stationära datorer, kraftförstärkare och professionell ljudutrustning.Dessa högimpedansmodeller matchar bra med utgångsfunktionerna för elektronik av professionell kvalitet.När du använder dessa hörlurar är det avgörande att justera volymen gradvis för att undvika överbelastning och skada de känsliga inre komponenterna, till exempel röstspolen.
Omvänt föredras hörlurar med låg impedans, vanligtvis under 50 ohm, för bärbara enheter som CD-spelare, MD-spelare eller MP3-spelare.Dessa hörlurar kräver mindre kraft för att leverera ljud av hög kvalitet, vilket gör dem idealiska för mobil användning.De kräver emellertid också noggrann uppmärksamhet på känslighetsnivåer för att säkerställa optimal prestanda och förhindra skador på hörlurarna eller hörseln.

Bild 8: Impedansdiagram över RC -seriekrets
Tillträde och analysförfaranden för RC -seriekretsar
Tillträde mäter hur lätt en RC -seriekrets kan genomföra el, beräknat som omvänd impedans ( ).Detta värde integrerar både motståndet (R) och reaktansen (X) av kretsen.Motståndet motsätter sig strömflödet genom att konvertera elektrisk energi till värme, medan reaktans lagrar energin tillfälligt i kretsen.
).Detta värde integrerar både motståndet (R) och reaktansen (X) av kretsen.Motståndet motsätter sig strömflödet genom att konvertera elektrisk energi till värme, medan reaktans lagrar energin tillfälligt i kretsen.
 ).Detta värde integrerar både motståndet (R) och reaktansen (X) av kretsen.Motståndet motsätter sig strömflödet genom att konvertera elektrisk energi till värme, medan reaktans lagrar energin tillfälligt i kretsen.
).Detta värde integrerar både motståndet (R) och reaktansen (X) av kretsen.Motståndet motsätter sig strömflödet genom att konvertera elektrisk energi till värme, medan reaktans lagrar energin tillfälligt i kretsen.För att beräkna tillträde
Börja med att skriva impedansen  , där R står för motstånd, X för reaktans och j är den imaginära enheten.Använd formeln y = 1/(R + jx).Denna operation involverar komplexa siffror och ger oss
, där R står för motstånd, X för reaktans och j är den imaginära enheten.Använd formeln y = 1/(R + jx).Denna operation involverar komplexa siffror och ger oss  .Här, G är konduktansen (faktisk strömflödesförmåga) och B är känsligheten (kretsens förmåga att reagera på strömförändringar).
.Här, G är konduktansen (faktisk strömflödesförmåga) och B är känsligheten (kretsens förmåga att reagera på strömförändringar).
 , där R står för motstånd, X för reaktans och j är den imaginära enheten.Använd formeln y = 1/(R + jx).Denna operation involverar komplexa siffror och ger oss
, där R står för motstånd, X för reaktans och j är den imaginära enheten.Använd formeln y = 1/(R + jx).Denna operation involverar komplexa siffror och ger oss  .Här, G är konduktansen (faktisk strömflödesförmåga) och B är känsligheten (kretsens förmåga att reagera på strömförändringar).
.Här, G är konduktansen (faktisk strömflödesförmåga) och B är känsligheten (kretsens förmåga att reagera på strömförändringar).
Bild 9: Serie RC Circuit Impedance Calculator
Denna beräkning avslöjar inte bara kretsens konduktivitet utan också dess dynamiska svaregenskaper, avgörande för AC -kretsanalys.Konduktans och känslighet, tillsammans, indikerar hur kretsen passerar ström och hur den lagrar och släpper energi.

Bild 10: Fasvinkelformel
Praktisk tillämpning
Ingenjörer använder tillträdesvärden för att förbättra kretskonstruktionen, särskilt i högfrekventa applikationer som radiofrekvenskretsar.Att justera tillträde hjälper till att matcha impedans, minska signalreflektionen och öka överföringseffektiviteten.
Genom att studera tillträdesresponsen kan ingenjörer bedöma och förutsäga kretsprestanda under olika förhållanden som frekvensrespons, stabilitet och känslighet.Utrusta med ett oscilloskop och en signalgenerator för att mäta kretsens spänning och ström vid olika frekvenser.Fokusera särskilt på avgränsningsfrekvensen för att testa teoretiska förutsägelser och validera dem mot praktiska observationer.För AC -kretsar börjar du med att bestämma kondensatorns reaktans (XC) med 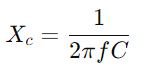 , var f är signalfrekvensen.Beräkna den totala impedansen
, var f är signalfrekvensen.Beräkna den totala impedansen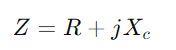 och sedan tillträde
och sedan tillträde  .
.
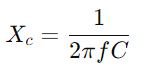 , var f är signalfrekvensen.Beräkna den totala impedansen
, var f är signalfrekvensen.Beräkna den totala impedansen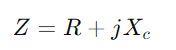 och sedan tillträde
och sedan tillträde  .
.Analysera fasskillnad med 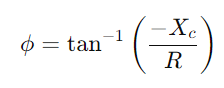 För att förstå förändring av signalform.Undersök hur kretsen hanterar olika frekvenser, särskilt och noterar beteendet vid avgränsningsfrekvensen
För att förstå förändring av signalform.Undersök hur kretsen hanterar olika frekvenser, särskilt och noterar beteendet vid avgränsningsfrekvensen  , där kretsen skiftar från att passera till blocksignaler.Utvärdering av hur impedans och fasskillnad varierar med frekvens är avgörande för att utforma effektiva filter och signalprocessorer.Diskutera hur frekvensselektivitet, fasförskjutningar och signaldämpning på grund av kretsens egenskaper påverkar praktiska tillämpningar som filtrering och elektronisk inställning.
, där kretsen skiftar från att passera till blocksignaler.Utvärdering av hur impedans och fasskillnad varierar med frekvens är avgörande för att utforma effektiva filter och signalprocessorer.Diskutera hur frekvensselektivitet, fasförskjutningar och signaldämpning på grund av kretsens egenskaper påverkar praktiska tillämpningar som filtrering och elektronisk inställning.
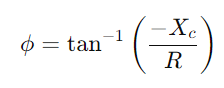 För att förstå förändring av signalform.Undersök hur kretsen hanterar olika frekvenser, särskilt och noterar beteendet vid avgränsningsfrekvensen
För att förstå förändring av signalform.Undersök hur kretsen hanterar olika frekvenser, särskilt och noterar beteendet vid avgränsningsfrekvensen  , där kretsen skiftar från att passera till blocksignaler.Utvärdering av hur impedans och fasskillnad varierar med frekvens är avgörande för att utforma effektiva filter och signalprocessorer.Diskutera hur frekvensselektivitet, fasförskjutningar och signaldämpning på grund av kretsens egenskaper påverkar praktiska tillämpningar som filtrering och elektronisk inställning.
, där kretsen skiftar från att passera till blocksignaler.Utvärdering av hur impedans och fasskillnad varierar med frekvens är avgörande för att utforma effektiva filter och signalprocessorer.Diskutera hur frekvensselektivitet, fasförskjutningar och signaldämpning på grund av kretsens egenskaper påverkar praktiska tillämpningar som filtrering och elektronisk inställning.Detta tillvägagångssätt delar upp de operativa processerna i hanterbara steg och berikar användarens förståelse med praktiska insikter om hantering och analys av RC -seriekretsar.

Bild 11: Egenskaper för RC -seriekretsar
Fasdiagram över RC -serien krets
I en RC -seriekrets har alla element samma ström på grund av deras seriekonfiguration.Denna enhetliga ström fungerar som en baslinje för vårt fasdiagram, vilket hjälper till att visualisera förhållandet mellan olika spänningar och strömmar i kretsen.Låt oss utse den här strömmen Jag som referensfasor, placerad i noll grader på diagrammet.I diagrammet, strömmen Jag är inställd horisontellt till höger och upprättar referenslinjen med noll grader.Spänningen över motståndet (UR) är i fas med strömmen eftersom motstånd inte orsakar någon fasförskjutning.Således, UR ritas som en horisontell vektor i samma riktning som Jag, sträcker sig från ursprunget.

Bild 12: RC Series Circuit Phasor Diagram
Däremot spänningen över kondensatorn (UC) leder strömmen med 90 grader på grund av den kapacitiva egenskapen att försena den nuvarande fasen.Denna spänning representeras av en vertikal vektor som pekar uppåt, börjar från spetsen på UR vektor.Den totala spänningen U i kretsen är vektor summan av U Rand UC.Denna summa bildar en höger triangel med UR och UC som de intilliggande respektive motsatta sidorna.Hypotenusen av denna triangel, som sträcker sig från ursprunget till spetsen på UC vektor, representerar U.
Den sinusformade strömmen genom kretsen ges av synd (ωt), där im är den maximala strömamplituden och Ω är vinkelfrekvensen.Följaktligen är spänningen över motståndet  , spegla den nuvarande vågformen.Spänningen över kondensatorn ges av
, spegla den nuvarande vågformen.Spänningen över kondensatorn ges av  , vilket indikerar en fasförskjutning på -90 ° (eller 90 grader före strömmen).Fasordiagrammets högra triangel klargör det
, vilket indikerar en fasförskjutning på -90 ° (eller 90 grader före strömmen).Fasordiagrammets högra triangel klargör det är inte bara i storlek utan också i fasförhållandet, med terminalspänningsvektorn (U) slutföra triangeln.
är inte bara i storlek utan också i fasförhållandet, med terminalspänningsvektorn (U) slutföra triangeln.
 , spegla den nuvarande vågformen.Spänningen över kondensatorn ges av
, spegla den nuvarande vågformen.Spänningen över kondensatorn ges av  , vilket indikerar en fasförskjutning på -90 ° (eller 90 grader före strömmen).Fasordiagrammets högra triangel klargör det
, vilket indikerar en fasförskjutning på -90 ° (eller 90 grader före strömmen).Fasordiagrammets högra triangel klargör det är inte bara i storlek utan också i fasförhållandet, med terminalspänningsvektorn (U) slutföra triangeln.
är inte bara i storlek utan också i fasförhållandet, med terminalspänningsvektorn (U) slutföra triangeln.
Bild 13: Spänningsfasdiagram över RC -seriekrets
Nyckelpunkter för att analysera serie RC -kretsar
Impedans i serie RC -kretsen, representerad som Z, kombinerar motstånd (R) och den reaktiva effekten av kapacitans till ett enda mått som varierar med signalfrekvens.Det uttrycks matematiskt som 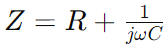 , var Ω är vinkelfrekvensen och C är kapacitansen.Här, R utgör den verkliga delen av impedansen, och
, var Ω är vinkelfrekvensen och C är kapacitansen.Här, R utgör den verkliga delen av impedansen, och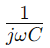 representerar den imaginära delen, vilket indikerar hur kondensatorn påverkar kretsen.
representerar den imaginära delen, vilket indikerar hur kondensatorn påverkar kretsen.
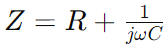 , var Ω är vinkelfrekvensen och C är kapacitansen.Här, R utgör den verkliga delen av impedansen, och
, var Ω är vinkelfrekvensen och C är kapacitansen.Här, R utgör den verkliga delen av impedansen, och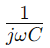 representerar den imaginära delen, vilket indikerar hur kondensatorn påverkar kretsen.
representerar den imaginära delen, vilket indikerar hur kondensatorn påverkar kretsen.Hur impedans förändras med frekvens är avgörande för att använda serie RC -kretsar vid filtreringsapplikationer.Vid lägre frekvenser uppvisar kretsen högre impedans, vilket effektivt blockerar dessa frekvenser.Omvänt, vid högre frekvenser, sjunker impedansen, vilket gör att dessa frekvenser passerar mer fritt.Detta beteende gör serien RC-kretsar idealiska för uppgifter som att filtrera bort oönskat lågfrekvent brus eller passera högfrekventa signaler.

Bild 14: Impedansvektordiagram över RC -serien krets
Slutsats
Från att filtrera oönskade frekvenser till formning av signalrespons är RC -seriens krets instrumental i ett brett spektrum av elektroniska funktioner.Genom att förstå de underliggande principerna som impedans, fasorförhållanden och frekvensberoende beteende hos dessa kretsar är ingenjörer och designers utrustade för hantverkslösningar som effektivt hanterar signalintegritet i komplexa elektroniska system.Den detaljerade undersökningen av dessa kretsar, som stöds av matematisk analys och visuella representationer som fasdiagram, erbjuder en omfattande insikt som är viktig för alla som vill fördjupa sin förståelse för elektronisk kretsdynamik eller för att förbättra deras praktiska färdigheter i kretsdesign och felsökning.
Vanliga frågor [FAQ]
1. Vad är principen för RC -kretsen?
Principen för en RC-krets (motståndskapacitor) kretsar kring laddnings- och urladdningsprocesserna för kondensatorn genom motståndet.I denna krets interagerar kondensatorns förmåga att lagra och frigöra elektrisk energi med motståndet, som styr hastigheten med vilken kondensatorn laddar eller släpps ut.
2. Varför leder en RC -krets ström?
I en RC -krets leder strömmen spänningen över kondensatorn eftersom kondensatorn måste börja ladda innan dess spänning kan stiga.Eftersom strömmen flyter in i kondensatorn för att ladda den, når de nuvarande topparna innan spänningen över kondensatorn sitt maximala.Denna effekt orsakar en fasförskjutning där den nuvarande fasen leder spänningsfasen med upp till 90 grader, beroende på insignalens frekvens.
3. Hur förändras spänningen i en RC -krets?
Spänningsförändringen i en RC -krets under laddning beskrivs av en exponentiell funktion.När en spänning appliceras ökar spänningen över kondensatorn initialt snabbt och bromsar sedan när den närmar sig matningsspänningen.Matematiskt uttrycks detta som 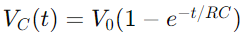 , var VC(t) är spänningen över kondensatorn vid tidpunkten t, v0 är matningsspänningen, och RC är kretsens tidskonstant, vilket bestämmer hur snabbt kondensatorn laddas.Omvänt, under urladdning, minskar spänningen över kondensatorn exponentiellt efter ekvationen
, var VC(t) är spänningen över kondensatorn vid tidpunkten t, v0 är matningsspänningen, och RC är kretsens tidskonstant, vilket bestämmer hur snabbt kondensatorn laddas.Omvänt, under urladdning, minskar spänningen över kondensatorn exponentiellt efter ekvationen 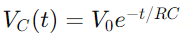 .
.
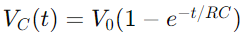 , var VC(t) är spänningen över kondensatorn vid tidpunkten t, v0 är matningsspänningen, och RC är kretsens tidskonstant, vilket bestämmer hur snabbt kondensatorn laddas.Omvänt, under urladdning, minskar spänningen över kondensatorn exponentiellt efter ekvationen
, var VC(t) är spänningen över kondensatorn vid tidpunkten t, v0 är matningsspänningen, och RC är kretsens tidskonstant, vilket bestämmer hur snabbt kondensatorn laddas.Omvänt, under urladdning, minskar spänningen över kondensatorn exponentiellt efter ekvationen 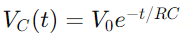 .
. OM OSS
Kundnöjdhet varje gång.Ömsesidigt förtroende och gemensamma intressen.
OM OSS
Kundnöjdhet varje gång.Ömsesidigt förtroende och gemensamma intressen.
funktionstest.De högsta kostnadseffektiva produkterna och den bästa tjänsten är vårt eviga engagemang.
Het artikel
- Är CR2032 och CR2016 utbytbara
- MOSFET: Definition, arbetsprincip och urval
- Reläinstallation och testning, tolkning av reläledningsdiagram
- CR2016 mot CR2032 Vad är skillnaden
- NPN vs. PNP: Vad är skillnaden?
- ESP32 vs STM32: Vilken mikrokontroller är bättre för dig?
- LM358 Dual Operational Amplifier Comprehensive Guide: Pinouts, Circuit Diagrams, Equivalents, användbara exempel
- CR2032 vs DL2032 vs CR2025 Jämförelsehandbok
- Förstå skillnaderna ESP32 och ESP32-S3 tekniska och prestandaanalys
- Detaljerad analys av RC -seriekretsen
 Fördjupad analys av 1N4148 Dioder: Driftslägen, specifikationer och användningsscenarier
Fördjupad analys av 1N4148 Dioder: Driftslägen, specifikationer och användningsscenarier
2024-05-08
 Förstå typerna och användningen av dynamiska och positiva förskjutningspumpar
Förstå typerna och användningen av dynamiska och positiva förskjutningspumpar
2024-05-07
Hett artikelnummer
 CGJ3E2C0G1H120J080AA
CGJ3E2C0G1H120J080AA C3216X7R2A224M115AA
C3216X7R2A224M115AA C3225C0G2A473K230AA
C3225C0G2A473K230AA 0402YD105KAT2A
0402YD105KAT2A AMK042BJ473MC-W
AMK042BJ473MC-W GRM2165C1H182JA01J
GRM2165C1H182JA01J CC0603DRNPO9BN5R0
CC0603DRNPO9BN5R0 CC0805GRNPO9BN152
CC0805GRNPO9BN152 1808SC102MAT1A
1808SC102MAT1A GRM0337U1H8R3CD01D
GRM0337U1H8R3CD01D
- TAP156M016SCS
- TAJD226K016H
- PIC32MX470F512L-I/PF
- MPC8247ZQTIEA
- MAX13174ECAG+T
- MAX845EUA+T
- ATMEGA164PA-AU
- ATUC128L4U-AUT
- Z8018006VEC
- BD7542FVM-TR
- V375C15T75BL
- VE-J6Y-EY
- V375A3V3C264AL1
- TPS73701DCQ
- ADM8828ARTZ-REEL7
- LM3S5T36-IQR80-C5
- AD5280BRUZ50
- NRVB230LSFT1G
- T491D107K016ZTZL11
- LM25011MYX/NOPB
- MSP430F1222IRHBT
- NCV59152DSADJR4G
- FAN7601BGX
- 74VHC139M-EL
- BD7710GWL
- BSP-15A/100-0004-22
- DS5002FP
- EP1K50FI484-2
- IS61SF12832-10TQ
- MB8AA4220-Z01-E1
- MC33128D
- PI6C2409-1HLX
- SP6660EU
- TK10489MTL
- AM99C10A-70JC
- VSP8801AZAKR
- LC4032V-75TN48C-XX00
- MT47H32M8BP-37EB
- DZAC000263